This post introduces the button keyboard, which is different from the piano keyboard. I will not introduce the piano keyboard here—it doesn’t need much explanation and is covered naturally in music theory (I have a post on that).
Stradella Bass System
Standard accordions typically use the Stradella bass system for the left-hand button keyboard. Unlike the piano keyboard, where each key corresponds to a single note, each button on the left-hand side of the accordion can produce either a single note or multiple notes—a chord.
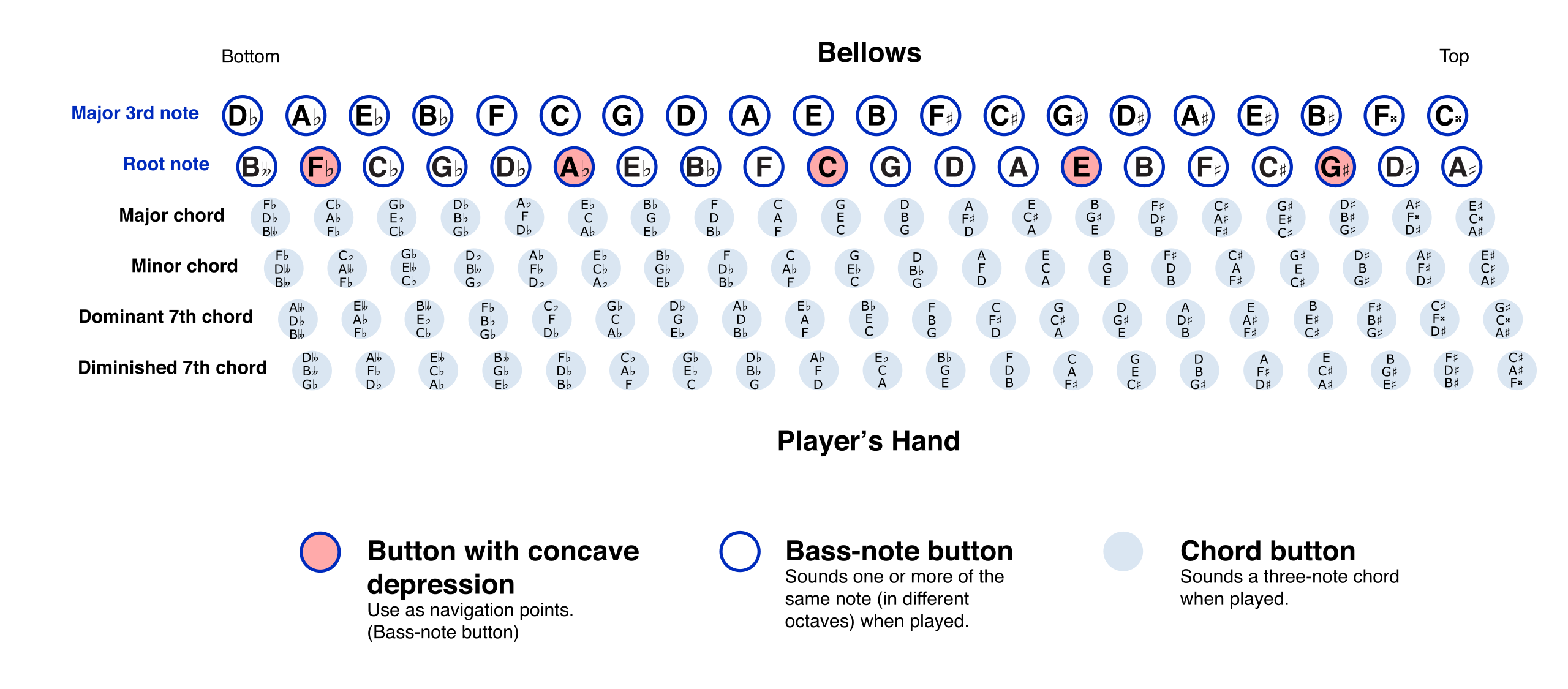
Figure 1 illustrates the layout of the Stradella system, which features fewer columns but more rows. We will explore it starting with the columns and then moving on to the rows.
First things first, it is important to emphasise that the accordion’s left-hand notes do not distinguish octaves (it is design as that). Because there are only 12 notes in an octave, the left hand can only produce 12 distinct notes.
Columns: Bass Notes and Chords
Each row of buttons represents a series of bass notes and chords built from a given root note. The columns are organised as follows:
Bass note button columns (1 note for 1 button):
- Root Bass Column: The 2nd column contains the root note of the row.
- Counterbass Column: The 1st column contains the counterbass note, which is a major third (4 semitones) above the root note in the same row.
Chord button columns (multiple notes for 1 button):
- Major Triad Chord Column: The 3rd column contains the major triad chord (root, major 3rd, 5th) built on the root note in the 2nd column of the same row.
- Minor Triad Chord Column: The 4th column contains the minor triad chord (root, minor 3rd, 5th) built on the root note in the 2nd column of the same row.
- Dominant 7th Chord Column: The 5th column contains the dominant 7th chord (root, major 3rd, minor 7th) with the 5th note omitted, built on the root note in the 2nd column of the same row.
- Diminished 7th Chord Column: The 6th column contains the diminished 7th chord (root, minor 3rd, major 6th) with the diminished 5th note omitted, built on the root note in the 2nd column of the same row.
Omitting the 5th note in the dominant 7th chord and the diminished 5th note in the diminished 7th chord are acceptable because the 5th note is not essential for identifying the chord. See my music theory (chords) post for more information.
For example, the C row in the middle contains the following buttons in order: E (the major 3rd of C), C (root note), C major chord, C minor chord, C7 chord, and C diminished 7th chord.
Rows: Circle of Fifths
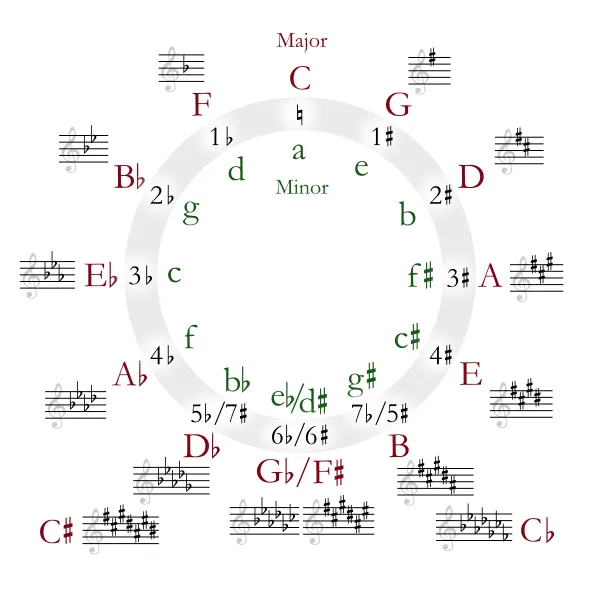
We have seen that each row is centred around a root note (located in the 2nd column). But how are these root notes arranged across the rows? The rows are organised according to the circle of fifths (Figure 2), with each row’s root note being a perfect fifth apart from its adjacent rows. For example, the C row is followed by the G row, then the D row, and so on; in the opposite direction, it is followed by the F row, then the Bb row, and so on. Because accordion left hand does not distinguish octaves, the rows repeat every 12 steps, meaning that buttons in the same column, spaced 12 rows apart, produce identical notes. This also complete a circle of fifths.
This design provides a significant advantage—key invariance, which is one of the most interesting features of this instrument. The relative positions of the left-hand notes remains consistent regardless of the key. Transposing to a different key only requires shifting the hand up or down, without altering the fingering or pattern. When learning the accordion’s left-hand system, you only need to master the pattern for one key. The patterns for other keys can be naturally derived by simply adjusting the hand position.
In contrast, the piano keyboard’s black and white keys result in distinct patterns for each of the 12 keys, requiring separate learning for each. For example, if you need to play Ab major scale in accordion left hand, you can simply move your hand playing C major scale to the Ab row (2 rows down, see Figure 3); but if you need to play Ab major scale in piano, you need to learn a completely different pattern completely different from C major scale.
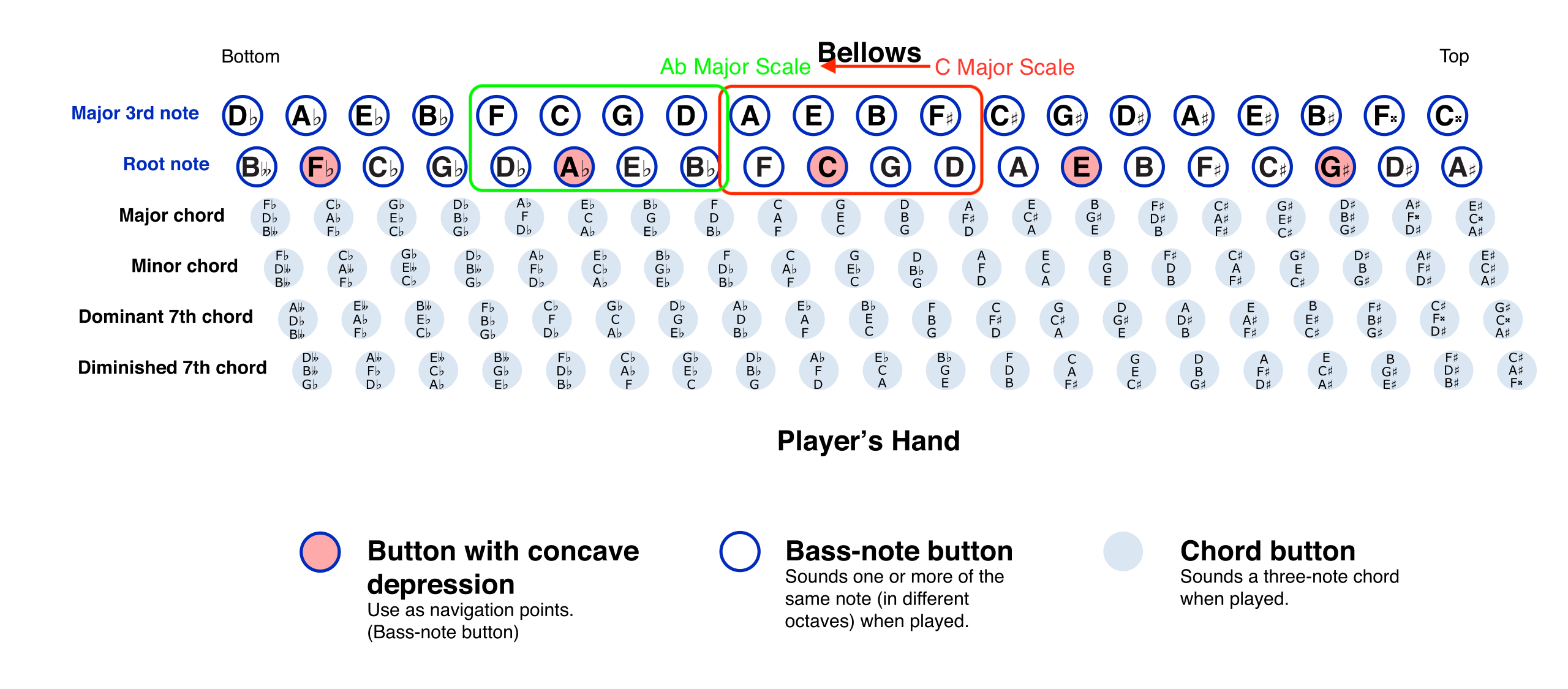
That’s why, from now on, everything with left hand only needs to be explained in only one key (you can imagine C key, the simplest), and other keys can be naturally derived.
Because of this property, in this and my other posts about the left-hand system (left-hand intervals, chords, scales, etc.), I will make the most from this concept—I use relative number representation that substitutes the absolute note names with intervals relative to a target note as the reference (similar to idea of numbered musical notation (简谱)):
| Number | Interval (Semitones) | Interval Name | Note in Key of C |
|---|---|---|---|
| 1 | 0 | Unison (Target Note) | C |
| 1# / b2 | 1 | Minor 2nd (Half Tone) | C# / Db |
| 2 | 2 | Major 2nd (Whole Tone) | D |
| 2# / b3 | 3 | Minor 3rd | D# / Eb |
| 3 | 4 | Major 3rd | E |
| 4 | 5 | Perfect 4th | F |
| #4 / b5 | 6 | Augmented 4th (Tritone) | F# / Gb |
| 5 | 7 | Perfect 5th | G |
| #5 / b6 | 8 | Augmented 5th | G# / Ab |
| 6 | 9 | Major 6th | A |
| #6 / b7 | 10 | Minor 7th | A# / Bb |
| 7 | 11 | Major 7th | B |
Note that the accordion left hand does not distinguish octaves, so only these 12 intervals are needed. In this relative number representation, “1” can represent any note, such as C, G, D, etc, which will correspond the whole thing to that C, G, D key.
To make this concept more intuitive, Figure 4 show the left-hand layout relative to a certain note. These representations are more practical and useful than the previous absolute note-based diagrams.
