Data Structure & Algorithm Takeaway: Binary Tree

What is a binary tree?

A binary tree is a special type of tree in which each node has at most two children, referred to as the left child and the right child.

What shapes can a binary tree take?

A binary tree can take various shapes, including:

Full binary tree: Every node has 0 or 2 children.
Complete binary tree: All levels are fully filled except possibly for the last level, which is filled from left to right.
Perfect binary tree: All internal nodes have two children and all leaf nodes are at the same level.

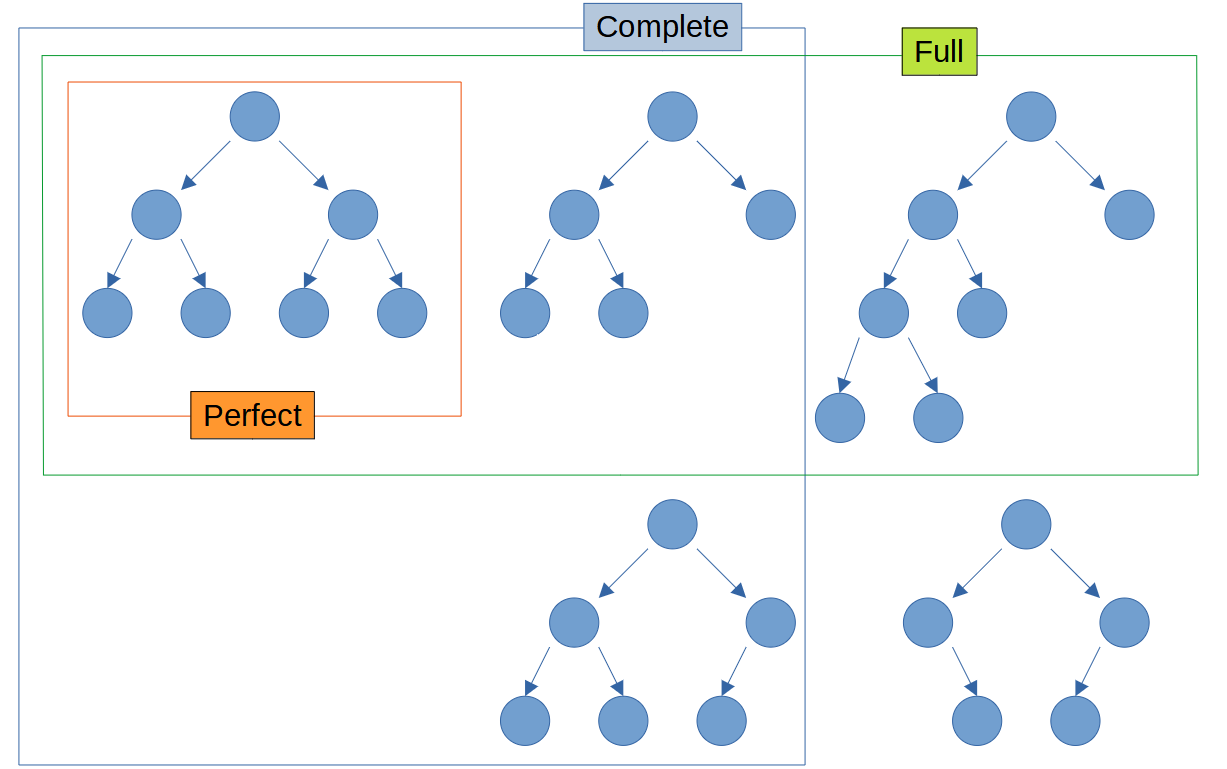
Full, complete and perfect binary tree. (Source: StackOverFlow)

Balanced binary tree: The height of the left and right subtrees of any node differ by at most one.
Skewed tree: All nodes have only one child, either left or right.
Degenerate (or pathological) tree: Each parent node has only one child, resembling a linked list.

How is a binary tree stored in memory (RAM)?

Linked binary tree representation. (Source: GeeksForGeeks)

A binary tree is typically stored in memory using a combination of nodes and pointers. Each node contains three parts: the data part, which stores the actual value of the node, and two pointer parts, which store the addresses of the left and right children. The root node is the topmost node in the tree, and each child node can have its own children, forming a hierarchical structure. The last nodes in the tree, called leaf nodes, do not have any children and their left and right pointers are set to null. This pointer-based representation for binary tree is called linked binary tree.

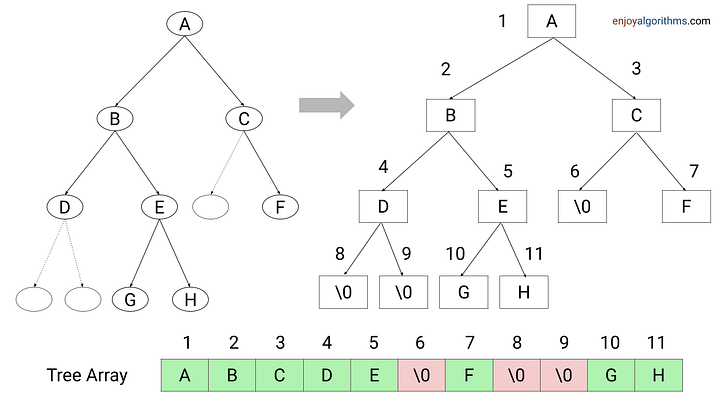
Array-based binary tree representation. (Source: Enjoy Algorithms)

The binary tree can also be represented using an array, where the root node is stored at index 0, and for any node at index i, its left child is stored at index 2i + 1 and its right child is stored at index 2i + 2. This array representation is particularly useful for complete binary trees, where all levels are fully filled except possibly for the last level, which is filled from left to right. This is called array-based binary tree.

What are pros and cons of linked binary tree and array-based binary tree?

The linked binary tree allows for dynamic memory allocation, making it easier to insert and delete nodes. However, it requires additional memory for storing pointers and can lead to fragmentation in memory.

The array-based binary tree is more memory-efficient and allows for faster access to nodes using index calculations. However, when the tree is not complete, it can lead to wasted space in the array, especially for skewed trees.

Is there any requirement for the element? Why?

All elements in a binary tree can be of different data types, because each node contains pointers to its children, allowing for a flexible structure.

What are the main operations of a binary tree?

The basic operations of a binary tree include:

Searching for an element: $O (n)$ in the worst case (when the element is not present or is at a leaf node)
Inserting an element: $O (n)$ in the worst case (when inserting at a leaf node)
Deleting an element: $O (n)$ in the worst case (when deleting a leaf node)
Traversing all elements: $O (n)$
- Get the depth of the tree: $O (n)$
- Get the number of nodes in the tree: $O (n)$
- Get the number of leaf nodes in the tree: $O (n)$

How to traverse a binary tree?

An example of traversing a binary tree. (Source: GeeksForGeeks)

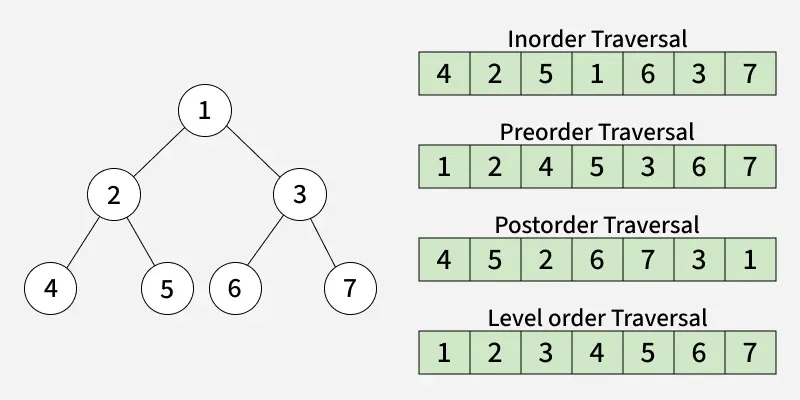
There are several different orders to traverse a binary tree:

Depth-First Search (DFS): This traversal method explores as far down a branch as possible before backtracking.
- In-order: In each subtree, visit the left child first, then the node itself, and finally the right child. This traversal order results in nodes being visited in ascending order for binary search trees.
- Pre-order: In each subtree, visit the node itself first, then the left child, and finally the right child. This traversal order is useful for creating a copy of the tree.
- Post-order: In each subtree, visit the left child first, then the right child, and finally the node itself. This traversal order is useful for deleting the tree.
Breadth-First Search (BFS): Traverse the tree level by level from top to bottom and left to right (also called level-order)

How to implement traversing a binary tree in Python?

Traversing a binary tree is essentially a special case of graph traversal, which uses DFS and BFS. The DFS algorithms can be implemented using recursion or using a stack data structure. The BFS algorithm can be implemented using a queue data structure.

Visiting nodes in binary trees seems very tedious, is there any way to simplify it?

There is a way to linearise a binary tree into a 1D sequence, which is called threaded binary tree. It still maintains the tree structure, but adds additional threads to the predecessor and successor of each node, allowing for easier traversal without using a stack or recursion.

First of all, the binary tree must be stored as a linked representation. Second, threaded binary tree only supports DFS order, that is in-order, pre-order, and post-order threaded binary trees.

Threaded binary tree is constructed when traversing the binary tree. We take in-order threaded binary tree as an example. When visiting a node, if its left child is null, we create a thread from the node to its predecessor; if its right child is null, we create a thread from the node to its in-order successor. It is not necessary to create a thread if it has a left or right child, because the predecessor or successor is already the left or right child.

Now we can see, a node’s left pointer can point to either its left child or its predecessor, and its right pointer can point to either its right child or its successor. We can simply use two boolean flags in each node to indicate whether the left or right pointer is a thread or a child pointer.

The tree with threads to the predecessors or successors only is called single threaded binary tree, and both predecessor and successor are called double threaded binary tree.