Data Structure & Algorithm Takeaway: Backtracking

What is backtracking?

Backtracking is a traversal search algorithm for solving combinatorial problems, particularly constraint satisfaction problem (CSP), that is, problems that involve finding all possible configurations or arrangements of a set of elements that satisfy certain constraints.

What is the input and output of a CSP?

In a constraint satisfaction problem (CSP), the input consists of:

Variables: A set of variables $v_{1}, v_{2}, \dots, v_{n}$ that need to be assigned values.
Domains: A set of possible values $V_{i}$ for each variable $v_{i} \in V_{i}$ .
Constraints: A set of rules that specify the relationships between the variables and the allowable combinations of values $C_{j} (v_{1}, v_{2}, \dots, v_{n}) = 0$ .

The output of a CSP is:

All possible complete assignment of values to all variables that satisfies all the constraints: $v_{1} = a_{1}, v_{2} = a_{2}, \dots, v_{n} = a_{n}$
If no such assignment exists, a declaration that no such assignment exists.

What is a vanilla solution to combinatorial problems?

A straightforward approach to solving combinatorial problems is to use a brute force search algorithm, which generates all possible combinations of the elements and checks each one to see if it satisfies the problem’s constraints.

for all possible $v_1 \in V_1$:
    for all possible $v_2 \in V_2$:
        ...
            for all possible $v_n \in V_n$:
                if configuration satisfies constraints:
                    add configuration to solutions

This approach is simple to implement but can be inefficient for large problems, as the number of possible configurations grows exponentially with the size of the input.

What is the relationship between backtracking and depth-first search (DFS)?

Backtracking is actually DFS in tree. Each node in the tree represents a partial solution to the problem, and the edges represent the choices that can be made to extend the partial solution. Below is a conceptual tree for a problem with three variables $v_{1}, v_{2}, v_{3}$ , each with domain ${a, b}$ .

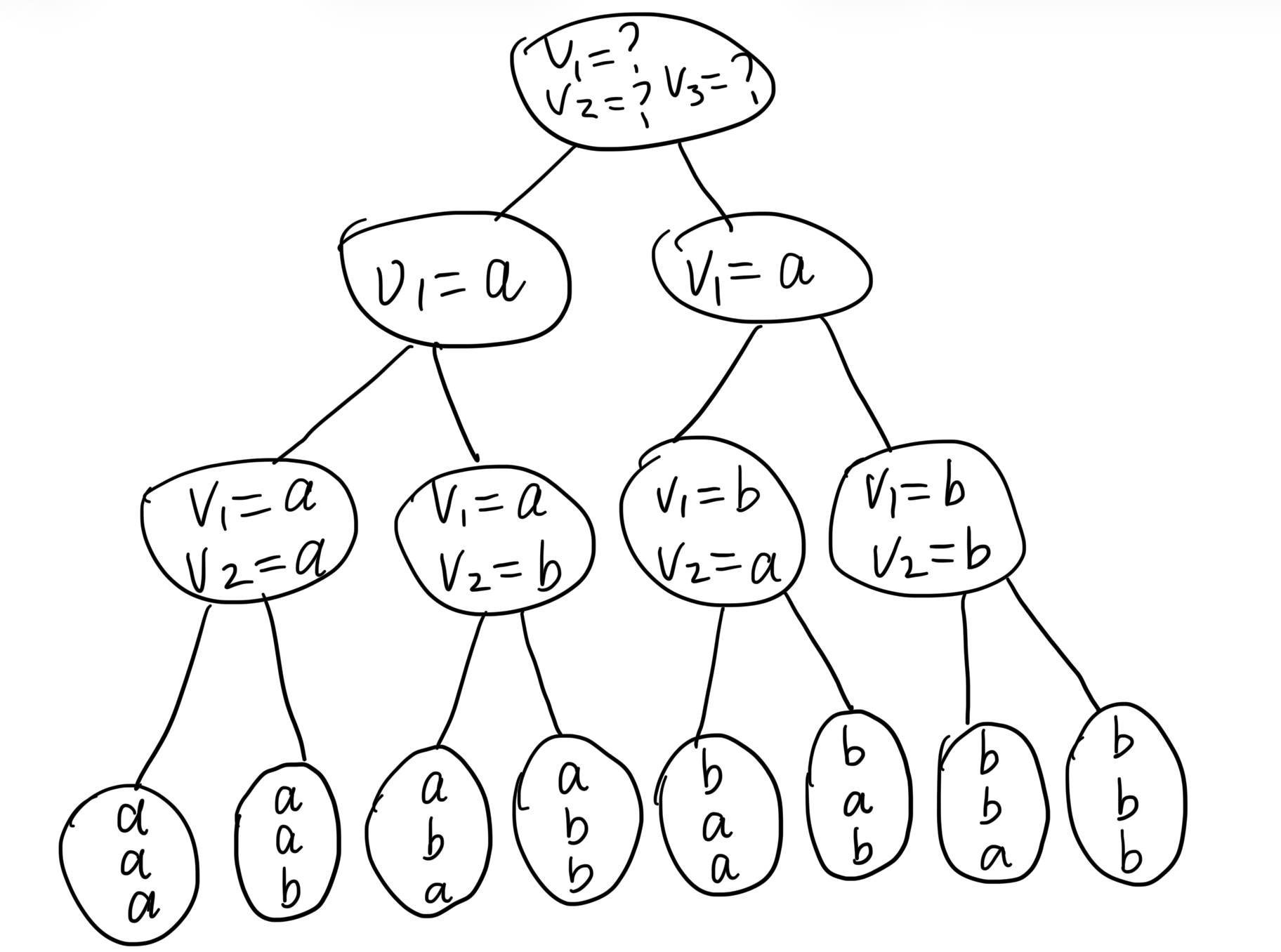
The difference between backtracking and DFS in a real tree is that backtracking deals with a conceptual tree that is not explicitly constructed in memory. The child node is based on the problem definition but not predefined tree structure.

The algorithm explores each branch of the tree by making a choice at each node, and if it reaches a dead end, it backtracks to the previous node and tries a different choice. In here, a dead end means that the partial solution cannot be extended to a valid solution, and thus the branch can be pruned.

How to implement backtracking?

The backtracking algorithm can be implemented using recursion:

function backtrack(partial_solution):

    if partial_solution is a complete solution:
        add partial_solution to solutions
        return

    // explore further
    for each choice that can be made to extend partial_solution:

        if choice is valid (does not violate any constraints):
            extend partial_solution with choice
            backtrack(partial_solution)
            undo_choice(partial_solution, choice)
        else:
            // prune the branch
            continue

Since backtracking and brute force are all search algorithms, why is backtracking more efficient?

In the tree representation of the problem, brute force search explores all nodes in the tree, while backtracking only explores the nodes that lead to valid solutions. If a partial solution cannot be extended to a valid solution, backtracking prunes that branch of the tree and does not explore it further. This pruning can significantly reduce the number of nodes that need to be explored, making backtracking more efficient than brute force search in many cases.

Please provide me a simple example of backtracking.

A classic example of a problem that can be solved using backtracking is the N-Queens problem, which involves placing $N$ queens on an $N x N$ chessboard such that no two queens threaten each other. The constraints for partial solutions are very straightforward that backtracking can prune the branches that violate the constraints early.

This can be formulated as a constraint satisfaction problem (CSP) as follows:

Variables: $v_{1}, v_{2}, \dots, v_{N}$ , where $v_{i}$ represents the column position of the queen in row $i$ .
Domains: $V_{i} = {1, 2, \dots, N}$ for each variable $v_{i}$ .
Constraints: No two queens can be in the same column or on the same diagonal.

The backtracking algorithm can be used to explore the possible configurations of the queens on the chessboard, pruning branches of the search tree that violate the constraints. The algorithm starts with an empty board and recursively places queens in each row, checking for conflicts with previously placed queens. If a conflict is detected, the algorithm backtracks to the previous row and tries a different column position for the queen.

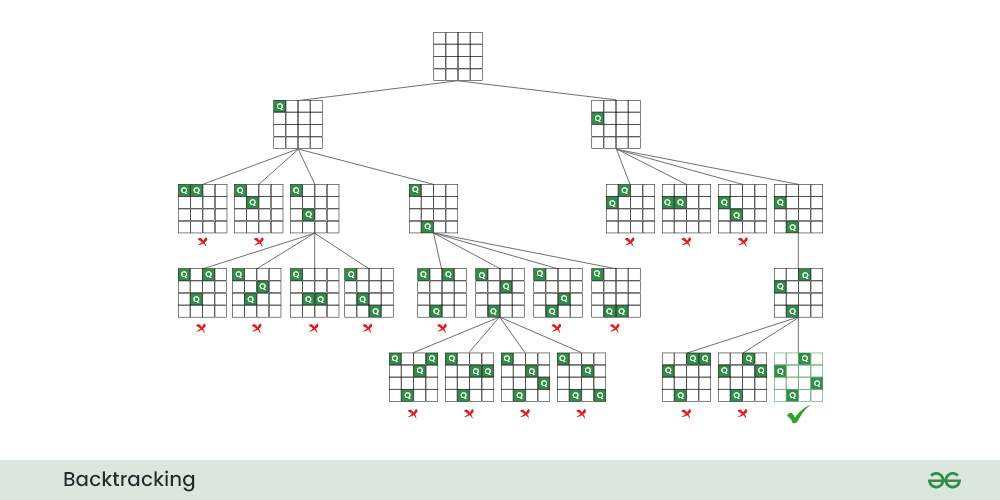
Backtracking N-Queens example. (Source: GeeksForGeeks)

In which scenarios can we use backtracking?

If a problem has the following properties, we can use backtracking to solve it:

Format: The problem requires an answer that is a set of choices, or a value that can be constructed from a set of choices (like the number of available choices).
Constraints: The problem has constraints that must be satisfied.
There is a easy way to decide whether a partial solution is valid or not, without having to complete the entire solution.