Data Structure & Algorithm Takeaway: Huffman Algorithm

TipWhat is Huffman algorithm?

Huffman algorithm is an algorithm to store weighted elements in a binary tree so that the elements with higher weights have shorter paths to access from the root. The binary tree constructed by this algorithm is called a Huffman tree.

TipWhat is the input and output of Huffman tree algorithm?

Input:

• A set of elements with weights: $a_1,a_2,\dots ,a_n$ with weights $w_1,w_2,\dots ,w_n$, where each weight is a non-negative value representing the importance or frequency of the corresponding element.

Output:

• A binary tree (Huffman tree) where each leaf node represents an element.

TipWhat is the objective of Huffman algorithm?

The objective of Huffman tree algorithm is to minimize the weighted path length from the root to all leaf nodes:

$$\text{Minimize }\sum _{i=1}^n{w}_i\cdot d_i$$

where $d_i$ is the depth of the leaf node representing element $a_i$ in the Huffman tree.

TipHow does Huffman algorithm work?

Huffman algorithm uses a greedy approach to build the Huffman tree. It takes the least two weighted elements, combines them into a new node with a weight equal to the sum of their weights, and repeats this process until there is only one node left, which becomes the root of the Huffman tree.

An example of constructing a Huffman tree. Source: Wikipedia

ImportantWhat is the time complexity of Huffman algorithm?

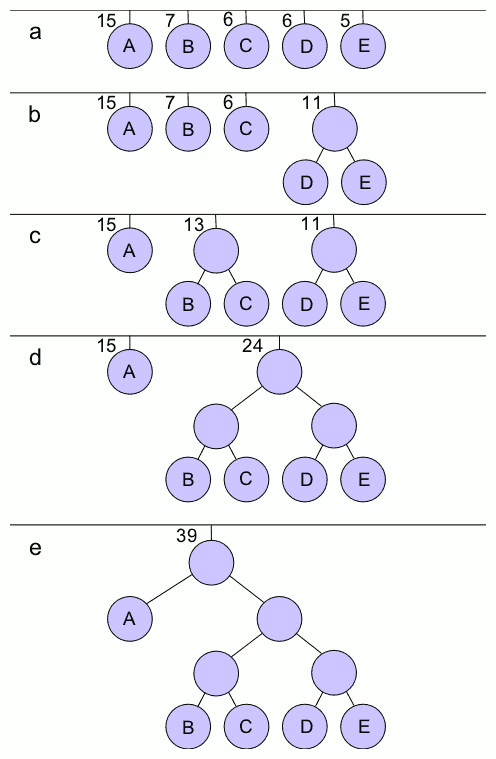
The Huffman algorithm steps seem easy with human eyes, but finding the two least weighted elements cannot be done directly in computer algorithm. A common approach is to use a priority queue (or min-heap) to efficiently extract the two minimum-weight nodes at each step, which takes $O(\log n)$ time for each extraction and insertion operation. Every step combines two nodes into a new parent node (1 node removed), so it is repeated $n-1$ times. Thus, the overall time complexity of the Huffman algorithm is $O(n\log n)$, where $n$ is the number of elements.

TipWhat are the applications of Huffman algorithm?

The most common application of Huffman algorithm is the Huffman coding, which is a lossless data compression algorithm that uses variable-length codes to represent symbols based on their frequencies. Huffman coding is widely used in various file formats and protocols, such as ZIP, JPEG, and MP3.

ImportantWhat is the input and output of Huffman coding?

Huffman coding is a mapping from input symbols to output codes.

Input:

• A set of symbols: $s_1,s_2,\dots ,s_n$.
• A set of reference frequencies (or weights) associated with each symbol: $f_1,f_2,\dots ,f_n$, where each frequency is a non-negative value representing how often the corresponding symbol appears in the data.

Output:

• A set of binary codes: $c_1,c_2,\dots ,c_n$, where each code is a unique sequence of bits (0s and 1s) assigned to the corresponding symbol.

Using these codes, one can encode a sequence of symbols (in the dictionary) into a binary string.

TipHuffman coding is variable-length encoding. How do we know where one code ends and the next code begins?

Huffman coding is prefix code, meaning that no code is a prefix of any other code. This property ensures that the encoded data can be uniquely decoded without ambiguity, as the end of one code can be determined by the start of the next code.

TipHow does Huffman coding work?

Huffman coding uses the Huffman algorithm to construct a Huffman tree based on the reference frequencies of the symbols. The binary code for each symbol is determined by the path from the root to the leaf node representing that symbol in the Huffman tree: moving left adds a ‘0’ to the code, and moving right adds a ‘1’.

An example of Huffman coding. (Source: GitHub)

TipWhy Huffman coding is a compression algorithm?

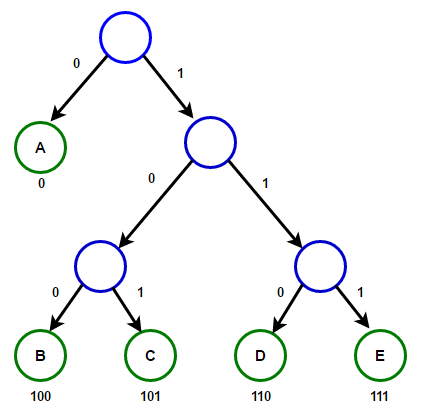
Symbols are originally stored in a fixed-length encoding scheme. Note that:

• The fixed-length encoding is also a prefix code (00…0 - 11…1, no overlap).
• Huffman algorithm is proven to minimize the weighted path length from the root to all leaf nodes, therefore, Huffman encoding is the optimal prefix code.

(Proof is omitted here, but you can find it in many algorithms textbooks or online resources.)

Thus, Huffman encoding will always produce a binary string that is shorter than or equal to the original fixed-length encoding, achieving lossless data compression.

TipWhy Huffman coding is lossless?

The decoding process of Huffman coding is straightforward: start from the root of the Huffman tree and traverse the tree according to the bits in the encoded data (0 for left, 1 for right) until reaching a leaf node, which represents a symbol. One can completely reconstruct the original symbol.